Compressible Flow

Module 4

4.1 Compressibility
4.2 Shock Waves
4.3 Flow through nozzles
4.4 Numerical Problems
4.1 Compressibility
Concepts of Compressibility
Compressible Flow
A flow is compressible when density changes are significant during motion. Typically important when M=a/V​>0.3, Where:M = Mach number,V = flow velocity, a=(γRT)(1/2) = speed of sound
Mach Number Regimes
Mach Number (M) Flow Regime
M < 0.3 Incompressible
0.3 ≤ M < 0.8 Subsonic
0.8 ≤ M < 1.2 Transonic
1.2 ≤ M ≤ 5 Supersonic
M > 5 Hypersonic
Thermodynamic Relations (Perfect Gas)
A perfect gas (or ideal gas) is a theoretical model of a gas where particles have negligible volume and no intermolecular forces, perfectly obeying the Ideal Gas Law (PV=nRT) under all conditions, meaning pressure (P), volume (V), and temperature (T) are directly related, and internal energy depends only on temperature.

1. Equation of State

p = ρRT

2. Specific Heats

cp − cv = R

γ = cp / cv

Typical values for air:
cp ≈ 1005 J/kg·K
cv ≈ 718 J/kg·K
γ ≈ 1.4

3. Internal Energy

u = cvT

du = cvdT

4. Enthalpy

h = u + pv = cpT

dh = cpdT

5. Speed of Sound

a = √(γRT)

6. Isentropic Relations

T2/T1 = (p2/p1)(γ−1)/γ
ρ2/ρ1 = (p2/p1)1/γ
T2/T1 = (ρ2/ρ1)γ−1

7. Entropy Change

ds = cp ln(T2/T1) − R ln(p2/p1)
ds = cv ln(T2/T1) + R ln(v2/v1)

Assumptions of Perfect Gas Model
  • Gas molecules have negligible volume
  • No intermolecular forces exist between gas molecules
  • Specific heats cp, cv, and ratio of specific heats γ are constant
  • Model is valid at moderate temperatures and pressures

SOPs to use calculator

Before using the calculator, ensure availability of the following parameters:

  1. Temperature, T (Kelvin, K)

  2. Pressure, p (Pascal, Pa)

  3. Velocity, V (meters per second, m/s)

  4. Gas Constant, R (J/kg·K)

  5. Ratio of Specific Heats, γ

    After calculation, the following outputs will be displayed:

    1. Density (ρ)

    2. Speed of Sound (a)

    3. Mach Number (M)

Thermodynamic Calculator (Perfect Gas)

Thermodynamic Calculator
(Perfect Gas)

4.2 Shock Waves

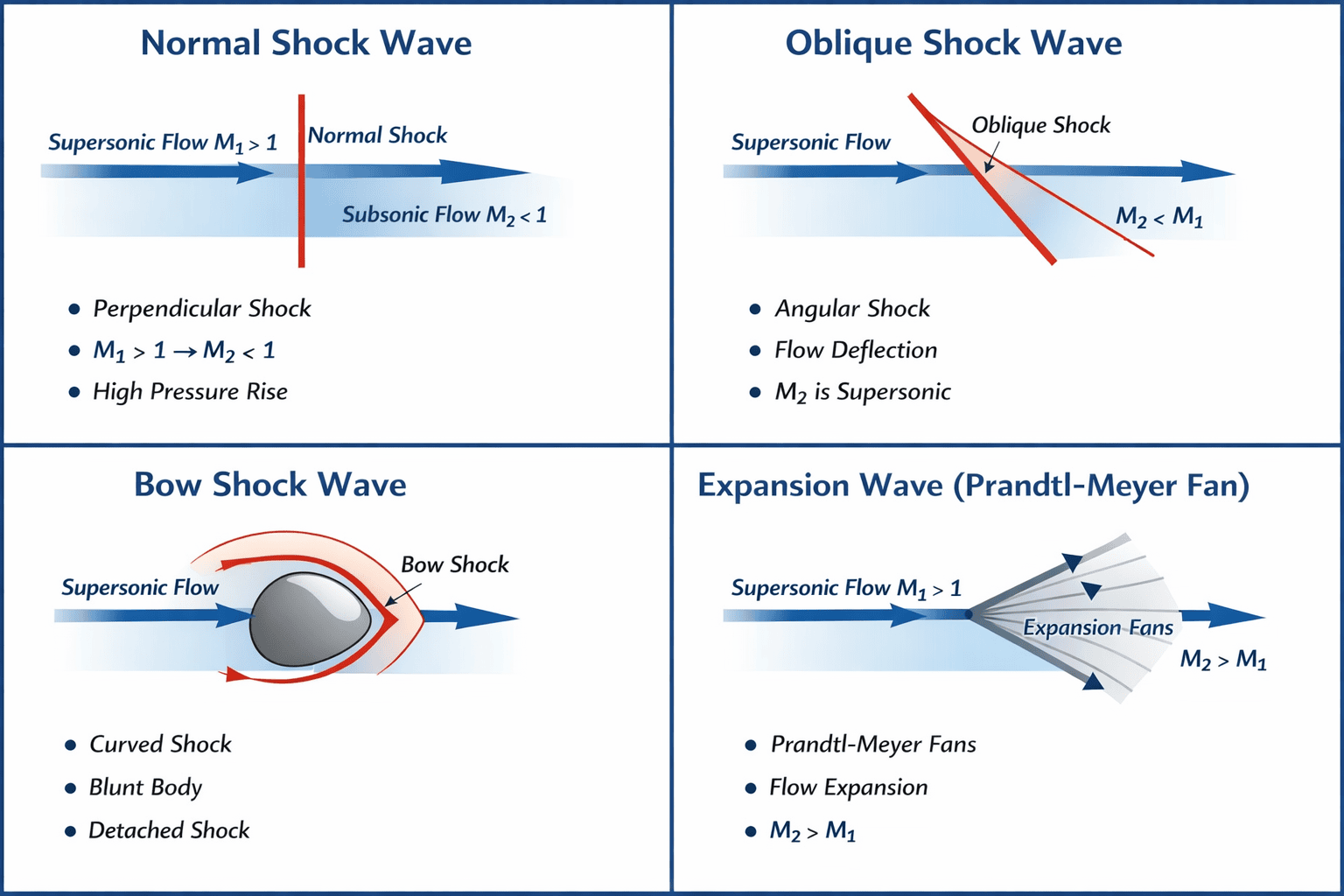
Concept of Shock Wave

A shock wave is a very thin region in a compressible flow where fluid properties change abruptly and irreversibly due to supersonic motion.

Key Characteristics

  • Occurs only when Mach number (M > 1)

  • Extremely thin (order of mean free path)

  • Causes entropy increase

  • Converts kinetic energy into thermal energy

Property Changes Across a Shock

  • Pressure ↑; Temperature ↑ ; Density ↑

  • Velocity ↓; Mach number ↓

Concept of Normal Shock Wave

A normal shock is a shock wave perpendicular to the direction of flow.

Where It Occurs

  • Inside convergent–divergent nozzles

  • In supersonic inlets

  • Ahead of blunt bodies at certain conditions

Flow Behavior

  • Supersonic flow becomes subsonic

  • Large pressure and temperature rise

Key Relations

  • Upstream Mach: M1>1>

  • Downstream Mach: M2<1

Energy Loss

  • High total pressure loss and Strong shock

Concept of Oblique Shock Wave

An oblique shock is a shock wave inclined at an angle to the flow direction.

Where It Occurs

  • Over wedges

  • At compression corners

  • Supersonic aircraft wings and inlets

Flow Behavior

  • Flow is turned toward itself

  • Mach number decreases but may remain supersonic

  • Weaker than normal shock

Key Angles

  • Shock angle (β) and Flow deflection angle (θ)

Special Case

  • When deflection angle increases → oblique shock becomes normal shock

Concept of Expansion Shock Wave

An expansion wave is a smooth, continuous flow expansion occurring when supersonic flow turns around a convex corner.

Nature

  • Isentropic process

  • Occurs as a fan of infinite weak waves

  • Reversible (no entropy increase)

Property Changes

  • Pressure ↓

  • Temperature ↓

  • Density ↓

  • Velocity ↑

  • Mach number ↑

Where It Occurs

  • Nozzle expansion

  • Trailing edges of wings

  • External expansion corners

4.3 Flow through nozzles

Compressible Flow Concepts

Flow through ducts

4.4 Numerical Problems

Numerical Problems


Developed by Dr. Aishwarya Dhara

Main Course
Course
Back
Next
Share -
Tags -